Блочная сортировка в Python

Введение

В этом руководстве мы рассмотрим теорию и практическую реализацию блочной сортировки в Python.

Блочная сортировка – это алгоритм, который распределяет элементы сортируемого списка по определенному количеству блоков (сегментов). После сортировки содержимое блоков добавляется, образуя отсортированную коллекцию.

Как работает блочная сортировка?

Сначала рассмотрим принципы работы блочной сортировки:

1. Создание блока для каждого элемента в массиве.
2. Перебор списка сегментов и добавление элементов из массива. В конечном итоге мы получим .n элементов в каждом блоке.
3. Сортировка каждого непустого блока. Так как мы работаем с небольшим набором данных, в каждом сегменте не будет слишком много элементов. Поэтому этот этап можно реализовать с помощью сортировки вставкой.
4. Перебор блоков по порядку. Когда содержимое каждого сегмента отсортировано, мы получаем список, в котором элементы расположены в соответствии с заданными критериями.

Теперь рассмотрим визуальное представление работы алгоритма. Предположим, что это входной список:

Самое большое значение в списке – 1.2. Размер списка – 6 элементов. Используя эти два значения, выясним оптимальный size для каждого сегмента. Для этого разделим наибольший элемент на длину списка. В нашем случае это 1.2/6, что даст 0.2. Разделив значение элемента на size, мы получим индекс для каждого сегмента соответствующего элемента.

Теперь создадим столько же блоков, сколько и элементов в списке.

Затем вставим элементы в соответствующие блоки. Так как 1.2/0.2 = 6, то индекс соответствующего сегмента будет равен 6. Если этот результат больше или равен длине списка, мы просто вычтем 1. Это происходит только с наибольшим значением. Так как мы получили size, разделив самый большой элемент на длину.

Мы поместим этот элемент в блок с индексом 5:

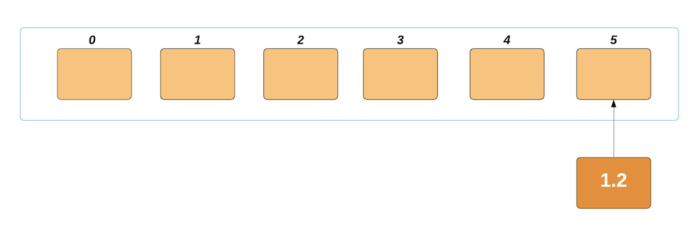
Следующий элемент будет проиндексирован 0.22/0.2 = 1.1. Так как это десятичное число, мы его округлим до 1 и поместим элемент во второй блок.

Этот процесс повторяется до тех пор, пока мы не поместим последний элемент в соответствующий блок. Теперь блоки будут выглядеть примерно так:

Теперь отсортируем содержимое каждого непустого блока с помощью сортировки вставкой.

Затем переберем непустые сегменты и объединим элементы в списке.

Реализация блочной сортировки в Python

Продолжим реализацию алгоритма с помощью Python. Мы начнем с функции bucket_sort():

def bucket_sort(input_list):
    # Находим максимальное значение в списке. Затем используем длину списка, чтобы определить, какое значение в списке попадет в какой блок
    max_value = max(input_list)
    size = max_value/len(input_list)

    # Создаем n пустых блоков, где n равно длине входного списка
    buckets_list= []
    for x in range(len(input_list)):
        buckets_list.append([]) 

    # Помещаем элементы списка в разные блоки на основе size
    for i in range(len(input_list)):
        j = int (input_list[i] / size)
        if j != len (input_list):
            buckets_list[j].append(input_list[i])
        else:
            buckets_list[len(input_list) - 1].append(input_list[i])

    # Сортируем элементы внутри блоков с помощью сортировки вставкой
    for z in range(len(input_list)):
        insertion_sort(buckets_list[z])
            
    # Объединяем блоки с отсортированными элементами в один список
    final_output = []
    for x in range(len (input_list)):
        final_output = final_output + buckets_list[x]
    return final_output

Сначала мы вычислили параметр size. Затем создали список пустых сегментов и вставленных элементов на основе их значений и параметра size каждого сегмента.

После вставки мы вызываем insertion_sort() для каждого из блоков.

def insertion_sort(bucket):
    for i in range (1, len (bucket)):
        var = bucket[i]
        j = i - 1
        while (j >= 0 and var < bucket[j]):
            bucket[j + 1] = bucket[j]
            j = j - 1
        bucket[j + 1] = var

Теперь заполним список и выполним сортировку.

def main():
    input_list = [1.20, 0.22, 0.43, 0.36,0.39,0.27]
    print('ORIGINAL LIST:')
    print(input_list)
    sorted_list = bucket_sort(input_list)
    print('SORTED LIST:')
    print(sorted_list)

Запуск этого кода вернет следующий результат:

Original list: [1.2, 0.22, 0.43, 0.36, 0.39, 0.27]
Sorted list: [0.22, 0.27, 0.36, 0.39, 0.43, 1.2]

Временная сложность блочной сортировки

Наивысшая сложность

Если у коллекции, с которой мы работаем, короткий диапазон – когда в одном контейнере много элементов с пустыми блоками.

Если все элементы попадают в один блок, временная сложность зависит исключительно от алгоритма, который используется для сортировки его содержимого.

При использовании сортировки вставкой ее временная сложность в худшем случае проявляется, когда список находится в обратном порядке. То есть: O (n 2).

Наименьшая сложность

Если все элементы уже отсортированы и распределены равномерно. Поэтому каждый блок будет содержать одинаковое количество элементов.

При этом создание сегментов заняло бы O(n), а сортировка вставки - O(k). Что дает временную сложность O(n + k) .

Средняя сложность

Встречается чаще всего, когда сортируемая коллекция случайная. В этом случае для завершения блочной сортировки требуется время O(n). Что делает ее очень эффективной.

Заключение

В этой статье мы узнали, что такое блочная сортировка. Затем реализовали алгоритм в Python и провели анализ его временной сложности.

Пожалуйста, оставляйте свои отзывы по текущей теме статьи. Мы крайне благодарны вам за ваши комментарии, отклики, дизлайки, подписки, лайки!